Chapter 9 Chapter 8: Crime along spatial networks
9.1 Introduction
In the previous chapter we explored how the techniques for spatial pattern analysis can be used to study the varying intensity of crime across space. We introduce the key idea of spatial randomness. These methods were developed to study locations in a continuous plane and are also referred to as planar spatial analysis. Point crime data, however, has an inherent structure to it. There are parts of our study region where it cannot appear. Since typically the data will be geocoded at the street level address, crime data almost always will appear alongside the spatial network of roads and streets. Crime won’t appear randomly anywhere in our 2 dimensional representation of the city, they will only appear along the street network covering this city. We can see this in the following example from Chicago using data from spatstat:
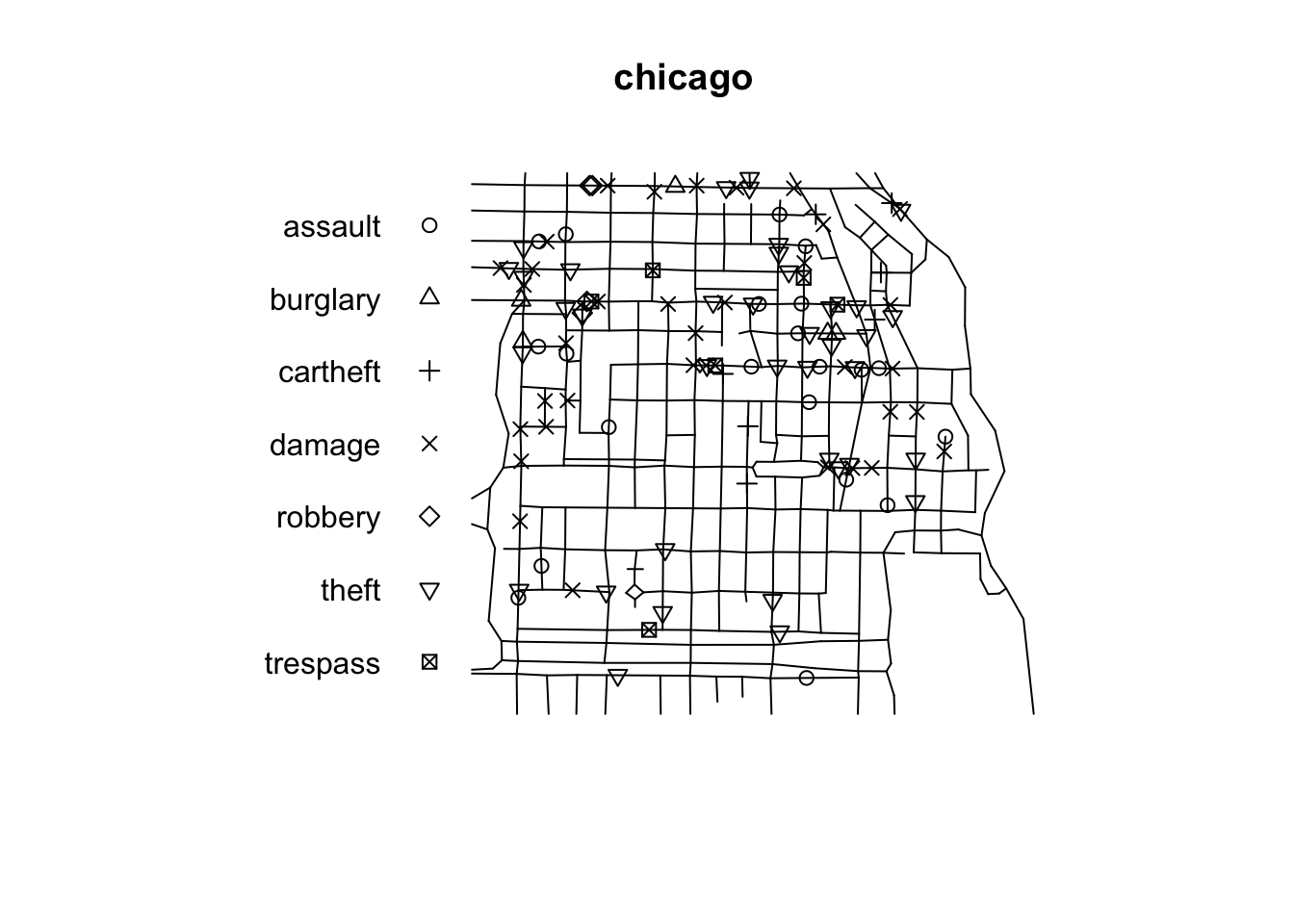
FIGURE 9.1: Crime along street networkin Chicago
Clearly the offenses are constrained to only occur along the street network. This has implications. This is not a homogeneous Poisson process along the whole study surface, because there is an underlying structure. If we want to investigate heterogeneity on intensity, for example, we would need to account for that underlying structure, the fact that the points can only be located along the network and not in other parts of the study region. Several authors have argued that crime is best represented and predicted if we focus in the street network rather than other kind of level of aggregation and that this has clear implications for operational policing (Singleton and Brunsdon 2014; Roser et al. 2017). It is clear that if our crime occurrences are collected and represented along a spatial network we need to ensure we use techniques of analysis and visualisation that respect this existing underlying structure in our data.
The software infrastructure for spatial analysis along networks, however, is still not as developed and consolidated. Partly this is to do with the statistical and computational challenges when we move from planar to linear network analysis. There is some software such as SANET that was originally conceived as a toolbox for ArGIS but with a beta standalone version already available (Okabe and Sugihara 2012). R users and developers are working to expand the functionality of R in this regard. It was only in 2020 that Lucas van der Meer, a Dutch spatial data scientist, published the first release of the sfnetworks package to facilitate the creation and analysis of spatial networks. Two other useful packages (SpNetPrep and DRHotNet) developed by Briz-Redón and colleagues are also only a couple of years old (Briz-Redón, Martı́nez-Ruiz, and Montes 2019a, 2019b). Another recent package, released in 2021, is spNetwork by Jeremy Gelb and Philippe Apparicio that can be used for kernel density estimation along networks (Gelb 2021). Finally, the package spatstat, that we covered in the last chapter, also provides functionality for the analysis of events along spatial networks.
In this chapter we will provide an introduction to the study of crime along networks by exploring the following:
- the creation of network representations from geographical vector objects
- linking data to meaningful micro-places such as street segment (or in our example, underground line segment) or street junction (or for us underground station)
- introducing the idea of hot routes
- evaluating crime concentration in these types of micro places using Gini coefficient and Lorenz curve
- street profile analysis - an alternative (non-spatial) way to visualise crime along a network
- introducing the functionallity of
spatstatfor the analysis of events along networks
# Packages for reading data and data carpentry
library(readr)
library(readxl)
library(janitor)
library(tidyr)
library(dplyr)
library(lubridate)
# Packages for handling spatial data
library(sf)
library(lwgeom)
library(sfnetworks)
library(spatstat)
library(spatstat.linnet)
library(rgdal)
library(maptools)
# Package for computing Lorenz curve
library(ineq)
# Packages for visualisation and mapping
library(ggplot2)
library(ggpubr)
library(leaflet)
# Packages providing accesss to spatial data
library(rnaturalearth)
library(osmdata)
library(tigris)
library(crimedata)It is not only in the case of street networks that understanding spatial point patterns along a network might be more meaningful, there are other networks we might want to consider. Transport networks are a good example of this and are receiving an increasing interest in criminology and crime analysis (Newton 2008; Tompson, Partridge, and Shepherd 2009; Ceccato 2013). Therefore we will focus on transport network scenarios throughout this chapter.
9.2 Constructing and storing a spatial linear network
The first difficulty one encounters when wanting to do analysis along spatial networks is to get the data for such geographical element in the proper shape. It is fairly straightforward to get files with the administrative boundaries for census geographies, as we have seen in previous chapters. This kind of geographical data is widely available in official and open repositories (see also Appendix C: sourcing geographical data for crime analysis). Getting data for spatial networks used to be a little bit trickier, although it is getting better. One could, for example, use the osmdata package to access Open Street Map data for a road network (we also discuss this in greater detail on Appendix C). Or, if you analyse data from the United States, you could use the tigris package to extract geometries which represent road networks.
Below we show how to obtain this data for Kensington, a popular neighbourhood in Toronto city centre through osmdata and for Manhattan using tigris. As we’re querying data from Open Street Map, first we draw a bounding box around the area we are interested in, then select “highways” as the feature to extract (see Appendix C for details on building OSM queries). As discussed by Abad, Lovelace, and Meer (2019), the osmdata package turns streets that form loops into polygons, to ensure we end up with lines we use osm_poly2line.
# using osm data
kensington_osm <- opq(bbox = c(-79.40772, 43.64726, -79.38672, 43.65986 )) %>%
add_osm_feature(key = 'highway') %>%
osmdata_sf() %>%
osm_poly2line()
kensington_lines <- kensington_osm$osm_lines %>% dplyr::select(highway)Now let’s use the tigris package to get TIGER/Line shapefiles from the United States Census Bureau. The roads() function returns the content of the all roads shapefile - which includes primary roads, secondary roads, local neighborhood roads, rural roads, city streets, vehicular trails (4WD), ramps, service drives, walkways, stairways, alleys, and private roads. It returns these as an sf object.
# using tigris
manhattan_roads <- roads("NY", "New York")We can now plot these two side by side
# plot results
plot_1 <- ggplot(kensington_lines) + geom_sf() + theme_void()
plot_2 <- ggplot(manhattan_roads) + geom_sf() + theme_void()
figure_1 <- ggarrange(plot_1, plot_2, labels = c("Kensington", "Manhattan"),
ncol = 2, nrow = 1)
figure_1
FIGURE 9.2: Street network geometries for Kensington in Toronto, CA and Manhattan, in New York, USA
What we have is two sf object containing linestrings. Linear networks indeed can be represented in R by simple features wit sf as here, or with the class SpatialLines of package sp. However, for us to be able to do particular kind analysis and some geospatial operations on this network we often will need a clear topology, we will need the data to be stored as a network graph. In other words, We need to move from linestrings to a linear graphical network representation, with edges (for example, representing street segments) and nodes (vertices indicating where they start and end).
This can be done by virtue of manual editing, which in large networks may be prohibitive, fully automatized, or automatized with manual edits just to correct errors. Explaining how to do this in detail with R would require space we do not have. Luckily, there are some good tutorials out there that you can consult for this data pre-processing work.
- Abad, Lovelace, and Meer (2019) explain how to use the packages
rgrass7andlink2GIfor this purpose. These packages bridge R to GRASS GIS software. So for this approach to work you would require this software also installed in your machine. Fortunately, GRASS GIS is freely available. - The vignettes for
sfnetworksalso cover how to turn a linestringsfobject into a network. The functionas_sfnetwork()provides the basic functionality for this. This package also includes several additional functions for cleaning the resulting network and there is a specific vignette documenting these (van der Meer et al. 2021). - Briz-Redón, Martı́nez-Ruiz, and Montes (2019a) developed the
SpNetPrep(“Spatial Network Preprocessing”). This package will open a Shiny application in RStudio that will allows for network creation and edition, network direction endowment and point pattern revision and modification. The key aim of this package is to allow for manual edits of the constructed network to correct for errors.
We quickly below show the as_sfnetwork() function with the road network in Kensington (which will generate an object of class sfnetwork) so that you get a sense for the look of a spatial network, but for further details on network construction and pre-processing it is important you see the documentation, as well as the other materials cited above.
kensigton_ntwk <- as_sfnetwork(kensington_lines)
plot(kensigton_ntwk)
FIGURE 9.3: Kengsinton as a spatial network
Once you have a spatial network that has been properly cleaned and prepared as discussed in the references above, there are a number of things you can do with it. You can apply geospatial operations, such as blending points into the edges, segmenting the edges, running spatial filters, etc. You can also apply standard social network analysis techniques and measures (such as centrality, measuring shortest path). Illustration of these applications are available in the vignettes for sfnetworks (van der Meer et al. 2021) and in Abad, Lovelace, and Meer (2019).
Another format for linear networks in R is linnet used by the package spatstat. When what we want is to do analysis not of the network itself, but of the location of points (such as crime events) along the network spatstat is the way to go and so we would need to ensure we store the data in formats that are required by this package. Statistical analysis of events along these networks is of key interest for crime analysts. Later in this chapter we will, for example, explain how to perform density estimation along networks. Until we get to that final section we will introduce applications of interest to crime analysis using, for convenience, slightly more standard and familiar data structures.
9.3 Visualising crime distribution along networks
To demonstrate some simpler approaches to visualising crime distribution along networks, we take open data from the British Transport Police (BTP), a national special police force that polices railways and light-rail systems in England, Wales and Scotland. Specifically, we will focus on crimes recorded by BTP on the London Underground system. Again, the data are available through the UK open police data portal and the geometry data from the Transport for London Open API, but we have also packaged these up with the data available for this textbook.
Let’s start with the crime data. Here the file you need is btp_crimes_2019.csv. We’ll also get a boundary for London for illustration purposes using the rnaturalearth package (see Appendix C for details on this package).
# get crimes data and clean up names
btp_crimes <- read_csv("data/btp_crimes_2019.csv") %>% clean_names()
# make the crimes data spatial and transform to projected coordinates
btp_crimes <- st_as_sf(btp_crimes, coords = c("longitude", "latitude"),
crs = 4326, agr = "constant") %>%
st_transform(27700) # transform to projected coords
# get a boundary for London from rnaturalearth package
ldn <- ne_states(country = "united kingdom", returnclass = "sf") %>%
filter(grepl("London", type_en) & name != "Derry") %>%
st_transform(27700) # transform to projected coordsNow we can have a look at our data by plotting it quickly
# plot the bountary and the crimes
plot(st_geometry(ldn))
plot(st_geometry(btp_crimes), add = TRUE)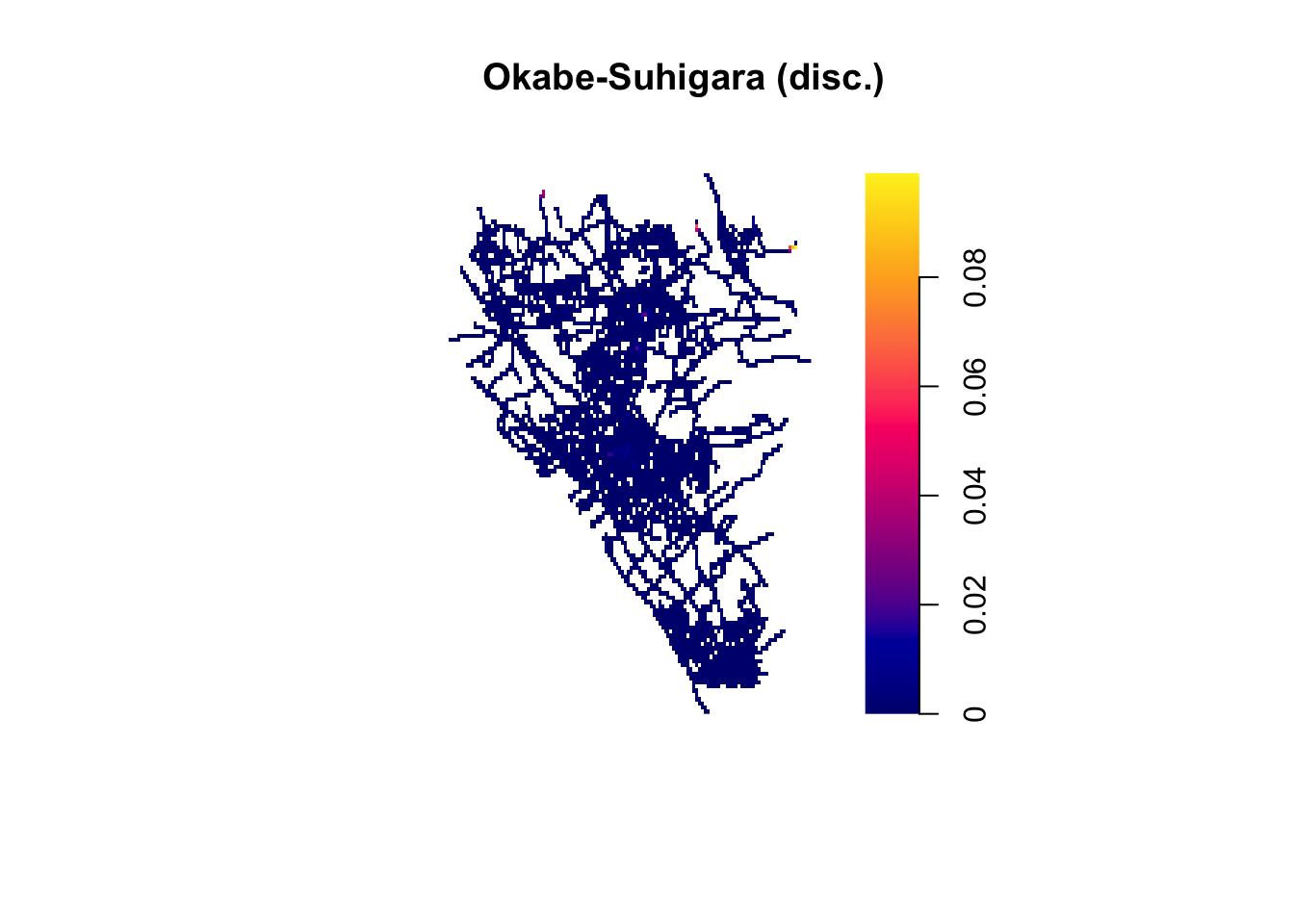
FIGURE 9.4: Crimes recorded by the British Transport Police in London
Here we can see the latitude and longitude locations of crimes in London recorded by British Transport Police. However, we know these must take place along the underground and rail network. So let’s see how we account for this in our analysis. For simplicity sake let’s focus on only one of the London Underground lines. We’ve picked the bakerloo line here. This is saved for you in two files. First the stations along the bakerloo line is in bakerloo_stops.csv, while the line is in the file bakerloo_line.geojson.
#read stops csv file
bakerloo_stops <- read_csv("data/bakerloo_stops.csv")
# make sf object
bakerloo_stops <- st_as_sf(bakerloo_stops,
coords = c("stn_lon", "stn_lat"),
crs = 4326) %>%
st_transform(27700) # transform to projected coordinates
# read bakerloo line geojson
bakerloo_line <- st_read("data/bakerloo_line.geojson",
quiet=TRUE) %>%
st_transform(27700) # transform to projected coordinatesYou can visualise the Bakerloo line here using ggplot2.
ggplot()+
geom_sf(data = bakerloo_stops) +
geom_sf(data = bakerloo_line) +
geom_sf(data = ldn, fill = NA) +
theme_void() 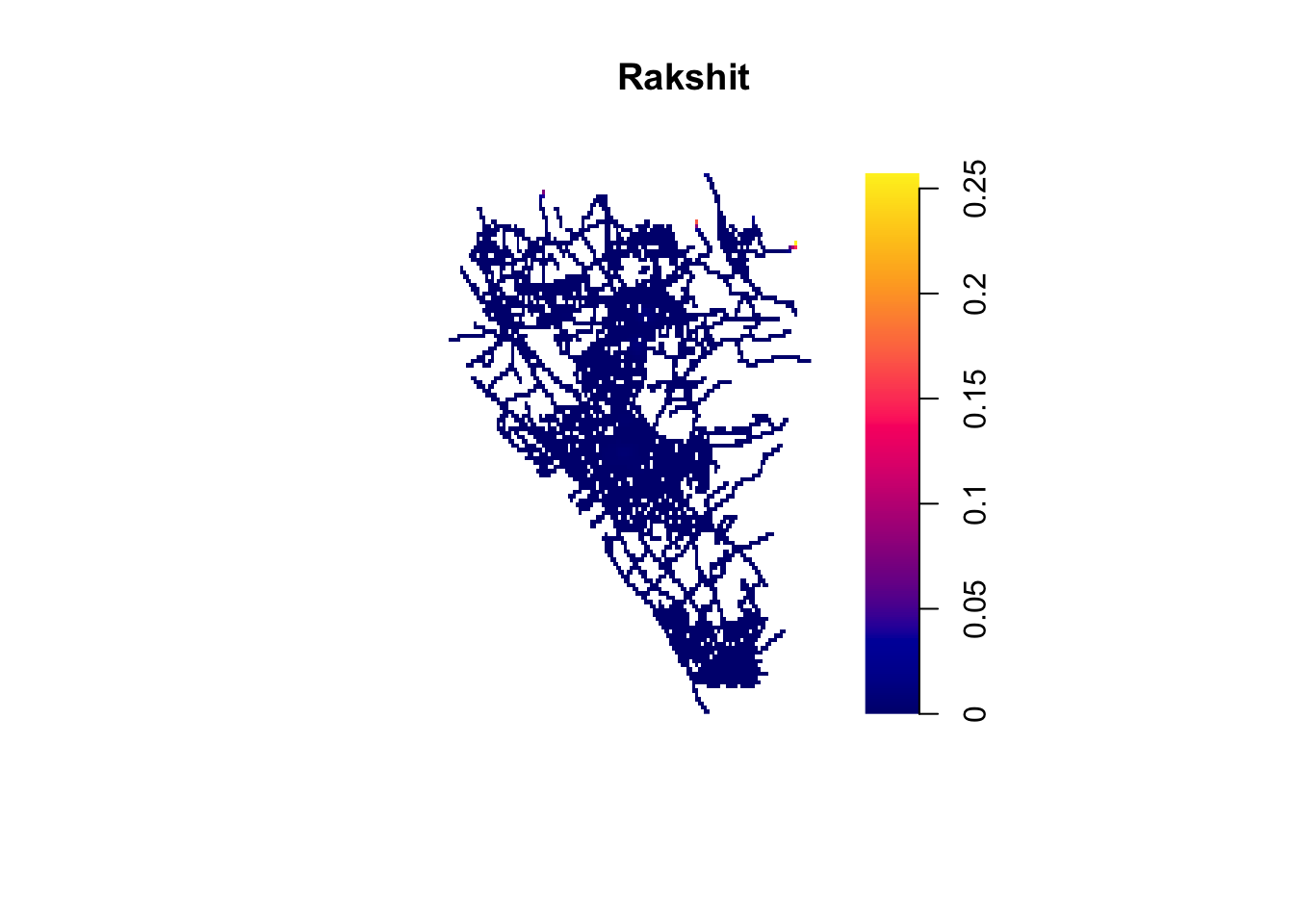
FIGURE 9.5: Bakerloo line in London
We can clearly see the nodes and the edges in this simplified network, all along this route.
9.3.1 Selecting relevant crimes for micro-places
For our demonstration, we will also need to select only those crimes which we can consider to have happened on (or near the Bakerloo Line). When carrying out your analysis you may have some flag or other variable in the data which indicates whether or not a crime occurred on or near a specific location. In the case of the police.uk data we have a column that we consider them to have happened on or near a specific location. This is the location column. If we have a glance you could see the sort of information it contains:
btp_crimes %>% dplyr::select(location) %>% head()We can see that these crimes occurred on or near Putney Bridge (Lu Station), Streatham Common (Station), Clapham Junction (Station). We can use this information to include only those stations which are on the Bakerloo line. We first need a list of all the station names. We can get this from our bakerloo_stops object which contains the names of the stations in the stn_name variable. In order to search for any of these station names, we can collapse them into an or string (separated by the | operator, which means or):
bk_sntns_list <- paste(bakerloo_stops$stn_name, collapse = "|")We can then use the grepl() function, which is a pattern matching function, which returns TRUE when a particular string is contained within another string. In other words, if the station name is in the location column. For example, if we are looking for crimes which occurred on or near Baker Street or Embankment we can paste them together with the or operator like this: Baker Street|Embankment, and then use this to find cases where either of these appear. If for example the location text said “On or near Oxford Circus,” we would not select this crime:
grepl("Baker Street|Embankment", "On or near Oxford Circus")## [1] FALSEBut if the crime occurred “On or near Baker Street” then we would:
grepl("Baker Street|Embankment", "On or near Baker Street")## [1] TRUEUsing the bk_sntns_list object we created above, which has all the stops along the Bakerloo Line, we can filter the whole btp_crimes object to include only those which occurred on or near them.
bakerloo_crimes <- btp_crimes %>% filter(grepl(bk_sntns_list, location))We can see a total of 4207 crimes can be attributed to having occurred on or near the stops of the Bakerloo Line. However, not all data sets will have such a handy location variable in the data set, and then we need to consider other ways of filtering only those crimes which are relevant to our specific micro places. One way is to use the spatial information available with our data, and perform spatial operations such as building a buffer and subsetting only those points which fall within a 200 meter buffer. (If not sure about the code below, see Chapter 2 Basic geospatial operations in R of this textbook for more detail and explanations for what is going on).
#create a buffer around the bakerloo_line object
bakerloo_line_buff <- st_buffer(bakerloo_line, 200)
# subset only those crimes which are located within this buffer
bakerloo_crimes <- st_intersection(bakerloo_line_buff, btp_crimes)You may see with this approach we have ended up with total of 4299 crimes. This number is different to what we got earlier, as we are probably erring on the side of including more crimes with a buffer - it may be that it happened on a station that falls on another line, but within the buffer we created. It is important to be aware of the strengths and limitations of the different approaches, and be explicit when drawing inferences from the data.
9.3.2 Assigning (joining) crimes to micro-places
Now that we have our relevant crimes, we want to join them to the appropriate micro-places. We will focus on line segments here. First, if we have a look at our line object, we have only one observation for the entire line. What we want is to break our line into sections. How you do this depends really much on what you want to show. In this case, it might be meaningful to consider each segment of the line between stops. In this case, we can use the shapefile of the stops (bakerloo_stops) to break up our line (bakerloo_line). However, as Tompson, Partridge, and Shepherd (2009) note, network layers typically contain streets of unequal length. This means that longer segments might show up as hot simply because they have more space to contain more crimes. Therefore in such cases it is advisable in this analysis to use equal length street segments, where possible. In this case however, let’s stick to the stops, as they create meaningful segments in our transport setting. To split our linestring (bakerloo_line) into many linestrings using the stops (bakerloo_stops) we can use the st_split() function from the lwgeom package and st_collection_extract() function from sf. Further, as the st_split() function is expecting a blade argument of length 1, we can use the st_combine() (from sf) function to group our tube stations altogether:
parts <- st_split(bakerloo_line, st_combine(bakerloo_stops$geometry)) %>%
st_collection_extract("LINESTRING")You can see we now have a new object called parts which is a linestring containing 24 features, the segments between our 25 tube stations, all as unique lines. You can also see that this is a geometry set of 24 features, let’s turn it into a simple features collection, and label each of the segments with a number by taking each element of parts and binding it together as a dataframe.
datalist = list()
for (i in 1:nrow(parts)) {
datalist[[i]] <- st_as_sf(data.frame(section = i),
geometry = st_geometry(parts)[i])
}
bakerloo_sections <- do.call(rbind, datalist)We now have the object bakerloo_sections which contains the 24 segments into which we sliced the bakerloo line, using the stops as points. The next step is to assign the points to each segment. Let’s first have a look at our data:
ggplot()+
geom_sf(data = bakerloo_sections) +
geom_sf(data = bakerloo_stops) +
geom_sf(data = bakerloo_crimes, col = "blue") +
theme_void() +
theme(panel.grid.major = element_line(colour = "white"))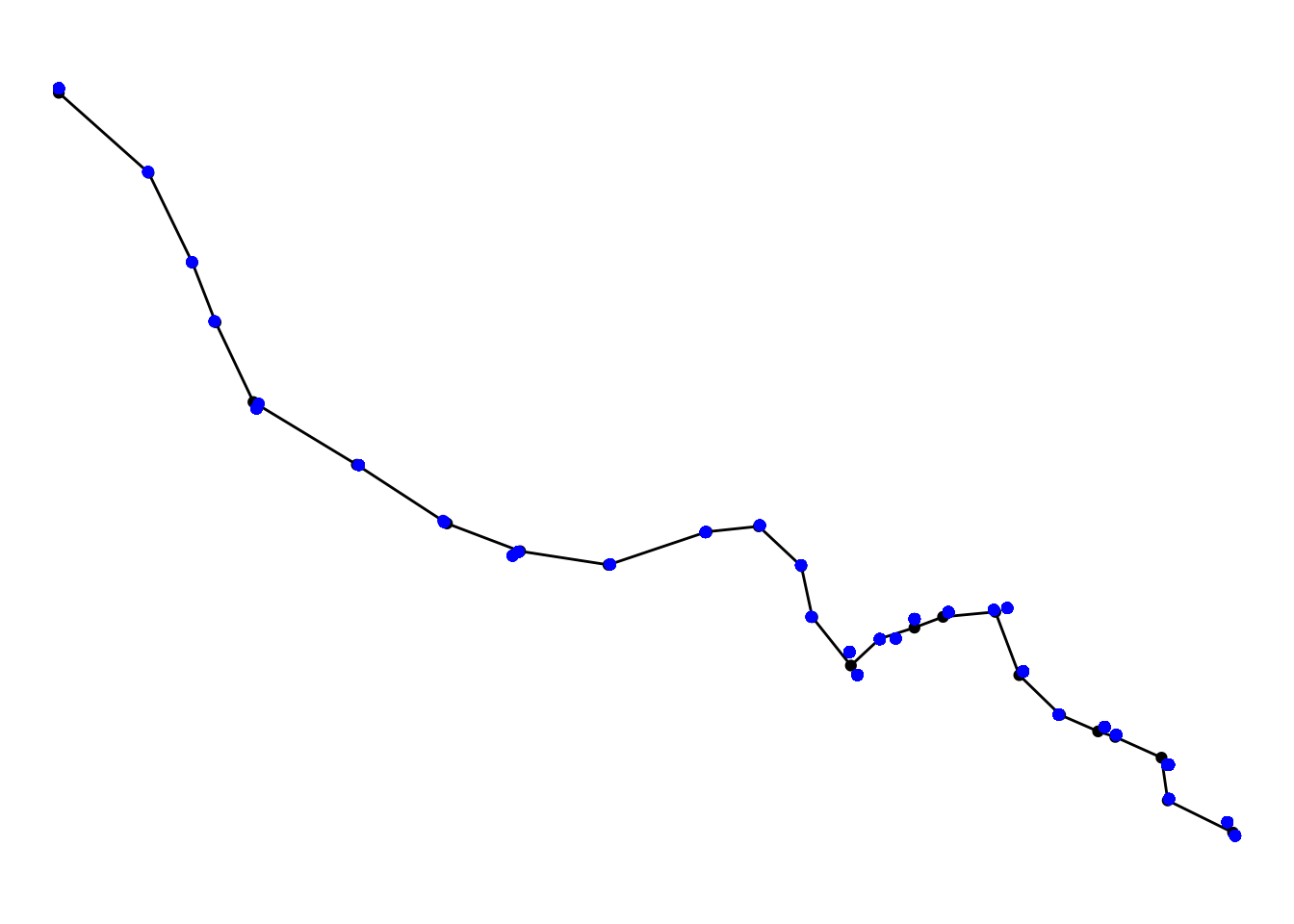
FIGURE 9.6: Crimes on or near Bakerloo line stations
Great, we see that we have the Bakerloo Line, its Stations, and only those crimes which we had deemed relevant. Now what we want to do is snap each one of these crime points to the nearest line section (remember we have the 24 sections in the parts object). To do this, we can use the st_nearest_feature() function. This will return, for each point, the ID of the nearest segment. This function is also covered in greater detail in Chapter 2 Basic geospatial operations in R of this textbook, so we won’t go into too much detail here.
bline_segments <- st_nearest_feature(bakerloo_crimes, bakerloo_sections)This new object is simply a list of the ID numbers of matched line segments for each of the 12 crime points in the bakerloo_crimes object. We can use this to create a frequency table and save this in a dataframe to be joined to the linesegment object. We will also need to replace our missing values with 0s, since in this case the segments which do not appear in our frequency table had 0 crimes snapped to them. For this, we use the replace_na() function from the tidyr package.
#make list of nearest into df of frequency
sections_freq <- as.data.frame(table(bline_segments))
#make sure id is numeric
sections_freq$bline_segments <- as.numeric(as.character(sections_freq$bline_segments))
#join to sections object and replace NAs with 0s
bakerloo_sections <- left_join(bakerloo_sections, sections_freq,
by = c("section" = "bline_segments")) %>%
mutate(Freq = replace_na(Freq, 0)) Now we have an sf object with each section labelled with the number of crimes that were snapped to it as they were the nearest segment. So essentially, the number of crimes on (and around, depending on your buffer decisions) each segment. We could map this count line:
# create midpoint object
midpoint_crimes <- mean(bakerloo_sections$Freq)
ggplot() +
geom_sf(data = bakerloo_sections, aes(colour = Freq), lwd = 2) +
geom_sf(data = bakerloo_stops) +
theme_void() +
scale_colour_gradient2(name = "Number of crimes",
midpoint = midpoint_crimes,
low = "#ffffcc", mid = "#fd8d3c", high = "#800026")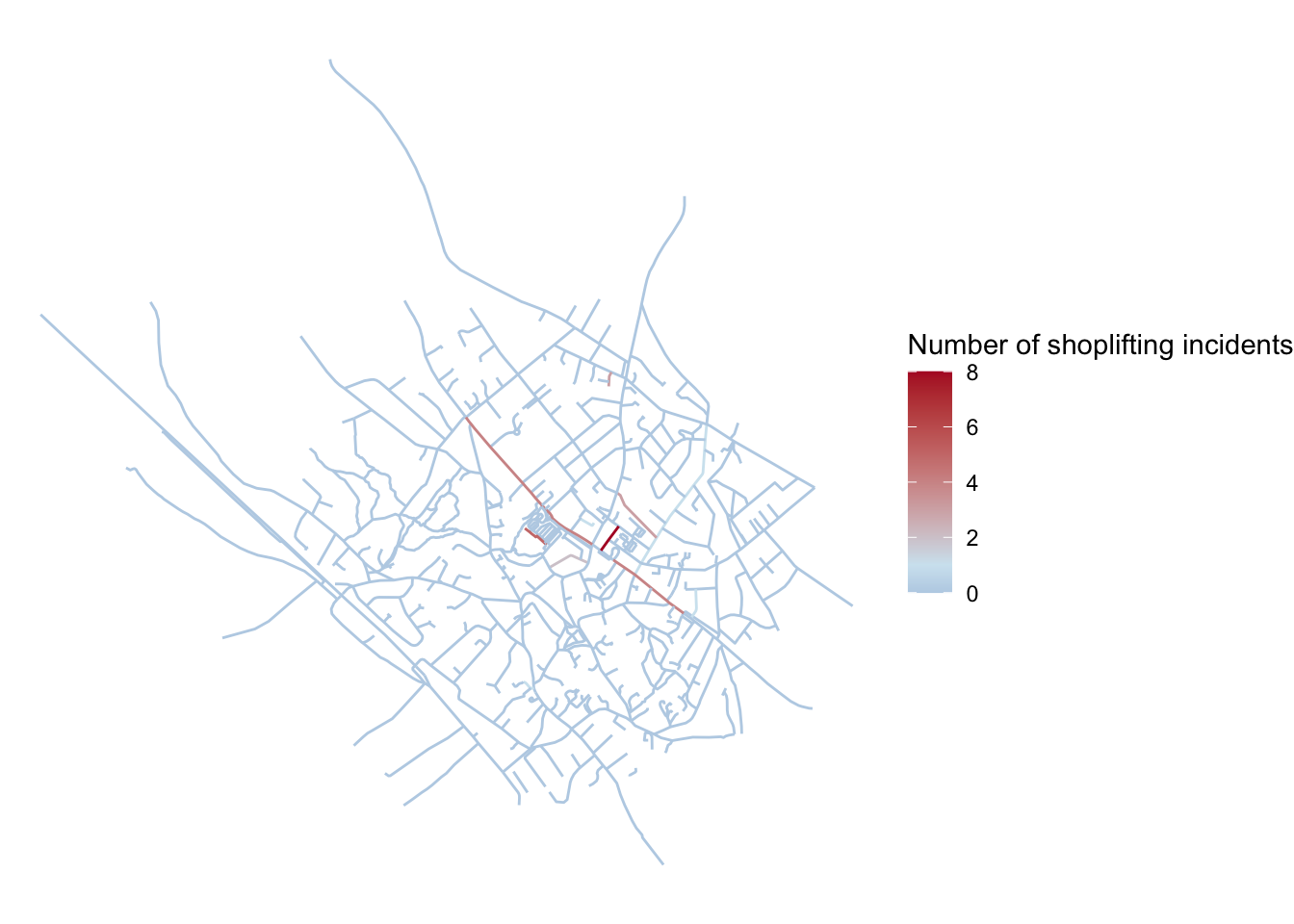
FIGURE 9.7: Hot routes map displaying count of crimes per segment
But of course we want to account for things like the length of each segment as they are unequal. We turn to that next.
9.3.3 Calculating a crime rate
For our comparison of crime along a network to be meaningful, we must calculate a crime rate. To calculate a rate we need a denominator. In this case, length may be a good one, so the length of each line segment needs to be calculated. We can do this using the st_length() function. Since our data are all in the British National Grid projection, this will return the length of each segment in meters.
bakerloo_sections$length <- st_length(bakerloo_sections)Once we have all the lengths, a new column needs to be created in the network layer to record a crime per metre score. This is calculated by dividing the number of crimes linked to a street segment by its length.
bakerloo_sections$crime_per_m <- bakerloo_sections$Freq / bakerloo_sections$lengthWe now have our crimes per meter score. We can then map this to create a proper map of hot routes.
9.3.4 Hot Routes
In order to map hot spots along a network, we can use a technique called hot routes. It was used by Newton (2008) to map crime and disorder on the bus network in Merseyside. A useful how-to guide was later produced by Tompson, Partridge, and Shepherd (2009). Hot Routes were devised to be a straightforward spatial technique that analyses crime patterns that are associated with a linear network (e.g. streets and other transportation networks). It allows an analyst to map crime concentrations along different segments of the network and visualise this through colour. We can create a Hot Routes visualisation by thematically shading each street segment with a colour (and line thickness if desired) that corresponds to the range of the rate of crime per metre. For this, let’s convert our crimes per meter (crime_per_m) variable to numeric from a “units” object, and then use ggplot once again.
bakerloo_sections$crime_per_m <- as.numeric(bakerloo_sections$crime_per_m)
midpoint_rates <- mean(bakerloo_sections$crime_per_m)
ggplot() +
geom_sf(data = bakerloo_sections, aes(colour = crime_per_m), lwd = 2) +
geom_sf(data = bakerloo_stops) +
theme_void() +
scale_colour_gradient2(name = "Rate of crimes per meter",
midpoint = midpoint_rates,
low = "#ffffcc", mid = "#fd8d3c", high = "#800026")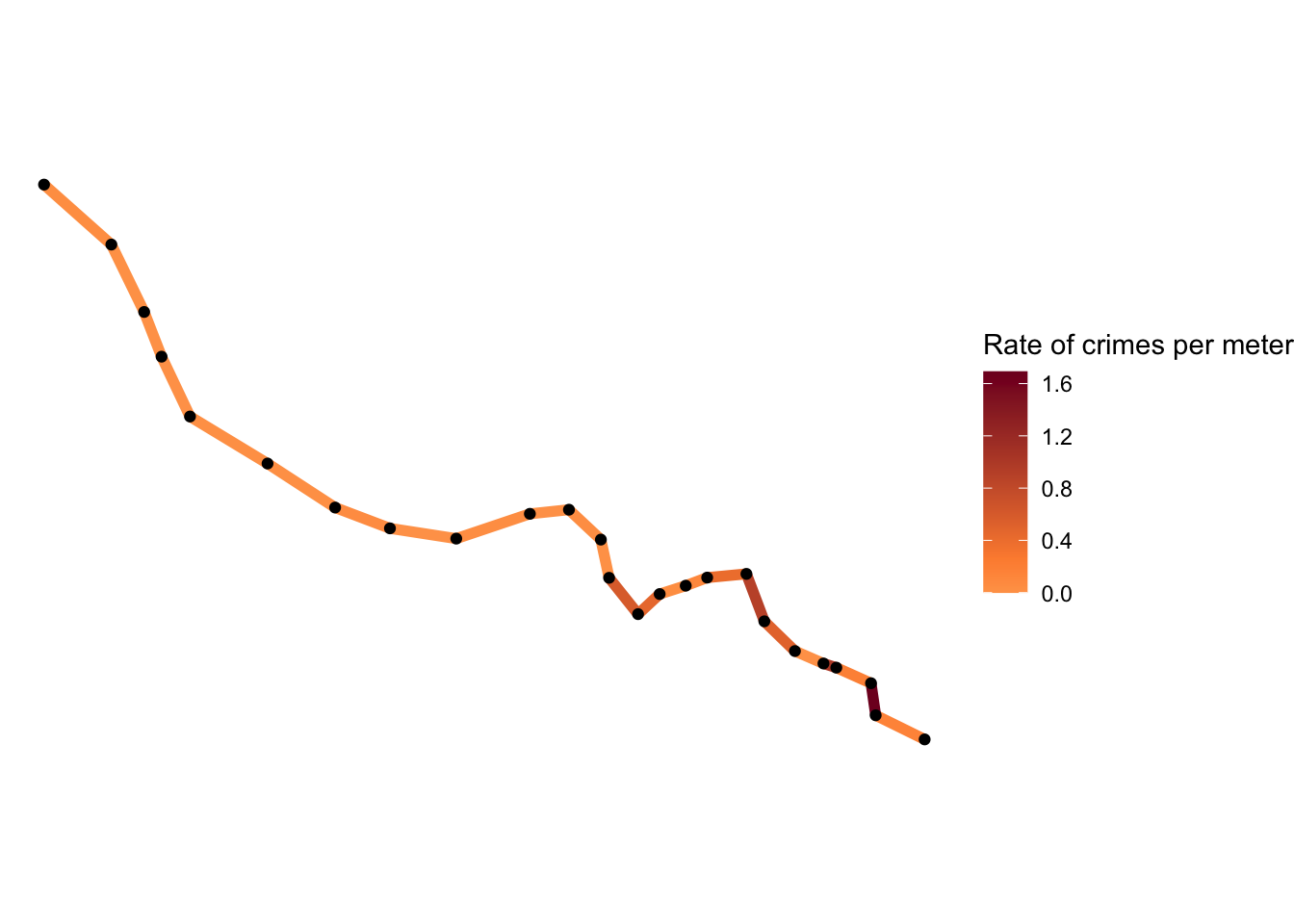
FIGURE 9.8: Hot routes map displaying rate of crimes per meter for each segment
We have now created a hot routes visualisation, that helps us map where crime rates are higher along a network. We can add some variations to this if we like, for example we could adjust the width of the segments as well as the colour:
ggplot() +
geom_sf(data = bakerloo_sections, aes(colour = crime_per_m, size = crime_per_m),
show.legend = "line") +
geom_sf(data = bakerloo_stops) +
theme_void() +
scale_colour_gradient2(name = "Rate of crimes per meter (colour)",
midpoint = midpoint_rates,
low = "#ffffcc", mid = "#fd8d3c", high = "#800026") +
scale_size_continuous(name = "Rate of crimes per meter (width)") 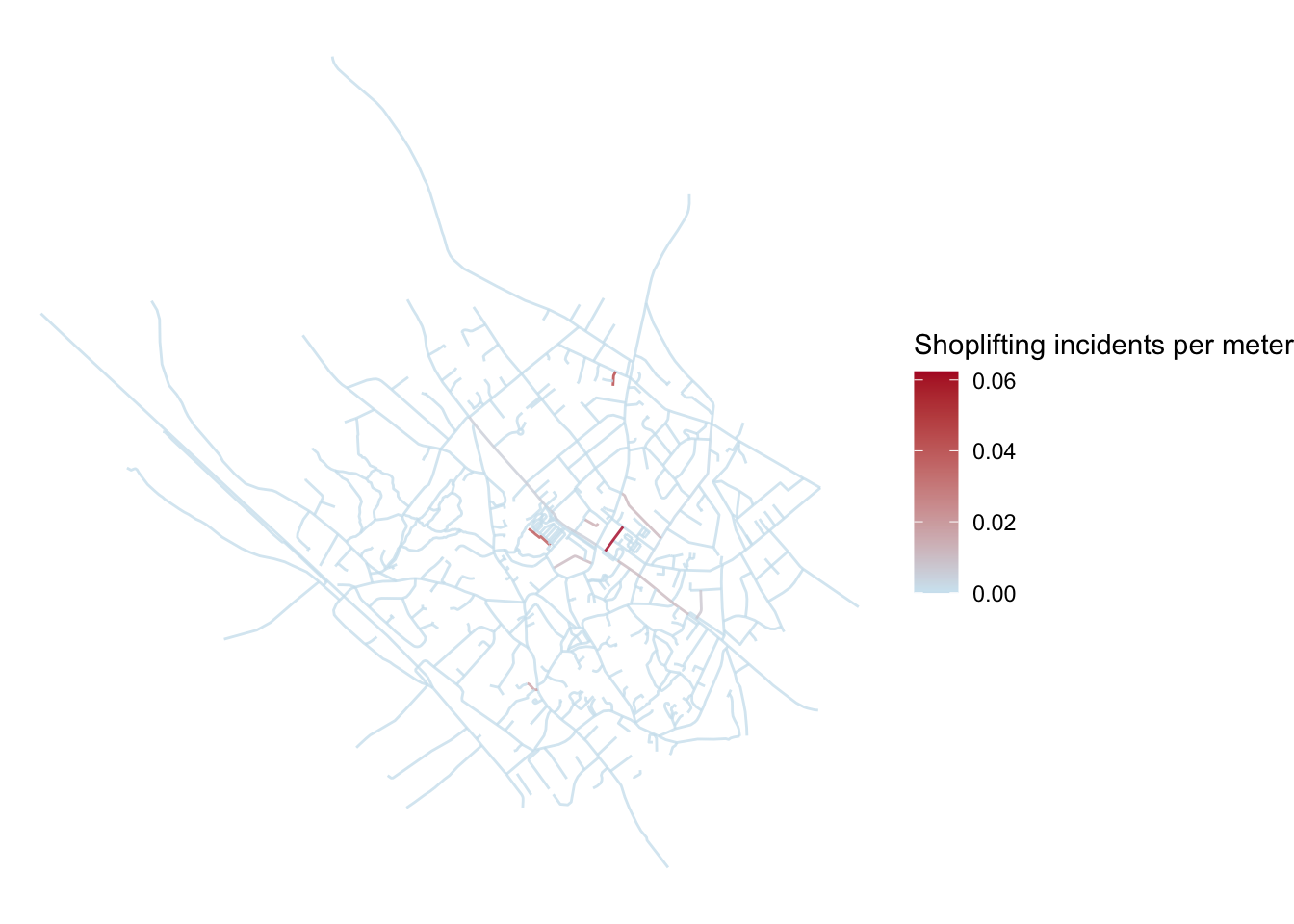
FIGURE 9.9: Hot routes map displaying rate of crimes per meter for each segment with line width as well as colour
Or we could consider alternative denominators besides the length of the segment, such as passengers, or trains, or other measures.
However we choose to display these hot routes maps, we can see they help identify where particular crimes might concentrate along our network of interest. But to what extent do we see crime concentrate on this network? To answer this, in the next section we look to quantify crime concentration at these micro-places.
9.4 Quantifying crime concentration at micro-places
In crime and place literature we explore the concentration of crime at micro places. “Perhaps the first and most important empirical observation in the criminology of place is that crime concentrates at very small units of geography” (Weisburd 2015, 135). A significant proportion of crime concentrates around a small proportion of micro places.
One way to measure inequality in the distribution of a quantitative variable is to use Lorenz curve, and associated Gini coefficient. The Lorenz curve is a probability plot (a P–P plot) comparing the distribution of a variable against a hypothetical uniform distribution of that variable. It can usually be represented by a function \(L(F)\), where \(F\), the cumulative portion of the population, is represented by the horizontal axis, and \(L\), the cumulative portion of the variable of interest (e.g. crime), is represented by the vertical axis. While Lorenz curves are used typically to graph inequality of distribution of wealth they can be applied in this case to explore unequal distribution of crimes between micro-places. A perfectly equal distribution would be depicted by the straight line \(y = x\). Zeileis, Kleiber, and Zeileis (2012). The corresponding Gini coefficient represents the ratio of the area between the line of perfect equality and the observed Lorenz curve to the area between the line of perfect equality and the line of perfect inequality (Gastwirth 1972). The closer the coefficient is to 1, the more unequal the distribution is (Zeileis, Kleiber, and Zeileis 2012).
In R we can implement these tests using the functions in the ineq package. To obtain a Lorenz curve, we can use the Lc() function. Lc() computes the (empirical) ordinary and generalized Lorenz curve of a vector \(x\) (in this case, our crimes_per_m variable). The function also computes a generalized Lorenz curve ( \(= \text{ordinary Lorenz curve} * mean(x)\)). The result can be interpreted like this: \(p*100\) percent account for \(L(p)*100\) percent of \(x\). Let’s illustrate with the segments of the Bakerloo line:
bk_lorenz <- Lc(bakerloo_sections$crime_per_m)Our resulting bk_lorenz object has 3 elements. First, the p represents the cumulative percent of crimes (per meter) for each line segment. Then, L contains the values of the ordinary Lorenz curve, while the L.general element the values for the generalised Lorenz curve. We can plot the Lorenz curve with the plot() function from base R.
plot(bk_lorenz)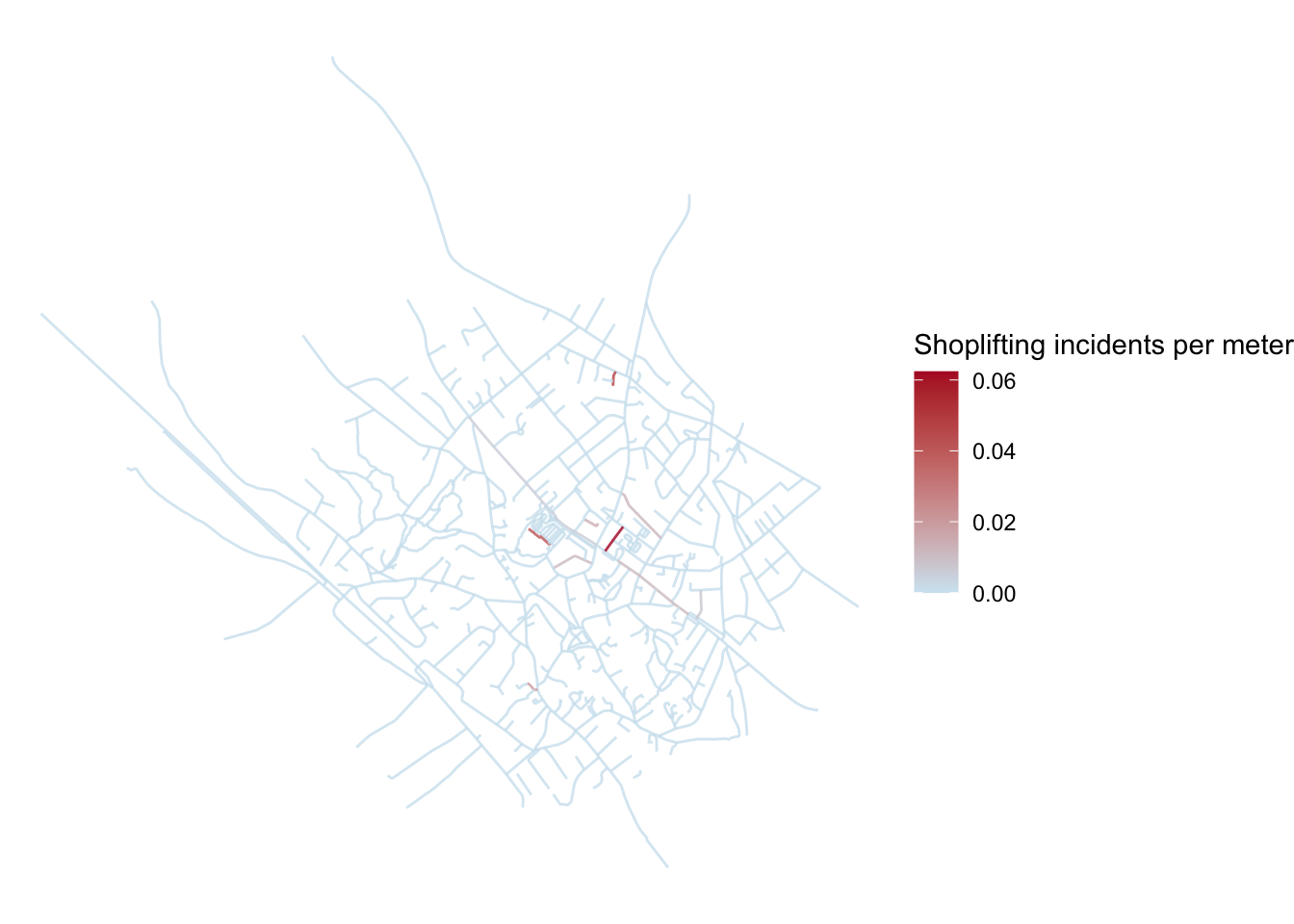
Upon seeing this, we can consider that many of the segments of the Bakerloo line contribute very little to overall crimes, and it is instead the top few which contribute most of the crimes. From a visual inspection, it appears that the Bakerloo line very precisely fits the Pareto Principle, whereby 20% of the segments seem to account for 80% of the crimes (per meter length of the segment). We can quantify this further using the Gini coefficient.
ineq(bakerloo_sections$crime_per_m, type="Gini")## [1] 0.7159This score of 71.6% is quite high. The Gini Index is calculated from the Lorenz curve, by taking the area between the line of equality and the Lorenz curve, and dividing this by the total area under the line of equality. This number is bounded between 0 (perfect equality where the Lorenz curve sits right on top of the line of equality) and 1 (perfect inequality, where the Lorenz curve sits right on top of the x axis and bends at right angle), so the closer we get to 1 the higher the inequality in the distribution in our value of interest, in this case crimes per meter. Clearly we see crime concentrate in certain segments of the Bakerloo line.
9.5 Street Profile Analysis
Visualising crime along networks presents an important first step in identifying crime concentration. It may not always be necessary to include the geographic component of a spatial network for the purposes of crime analysis in these networks. Instead, another approach could be to make use of street profile analysis introduced by Spicer et al. (2016). Street profile analysis was initially developed as a method for visualising temporal and spatial crime patterns along major roadways in metropolitan areas. The idea is that the geographical location of the street may not actually be as important as the ability to visualise data from multiple years in a comparable way. So the approach is to treat the street in question as the x-axis of a graph, with a start point (A) and end point (B) breaking it into some interval. Then, you can visualise how crime is distributed along this street by plotting count or rate of crimes on the y-axis, and have multiple lines for different years for example. You can add context by re-introducing some key intersections, or other points of interest. In their paper, Spicer and colleagues demonstrate this using the example of Kingsway Avenue in Vancouver, BC. In this section we will go through how we can apply street profile analysis in R.
9.5.1 Linking data to nodes
For street profile analysis (or let’s call it network profile analysis here, as we are applying this to the Bakerloo Line example), instead of linking the crimes to the nearest line segment, we actually want to link to the nearest station. To do this, we can go back to the stage where we had our line, our stops, and our relevant crimes:
ggplot()+
geom_sf(data = bakerloo_sections) +
geom_sf(data = bakerloo_stops) +
geom_sf(data = bakerloo_crimes, col = "blue") +
theme_void() +
theme(panel.grid.major = element_line(colour = "white"))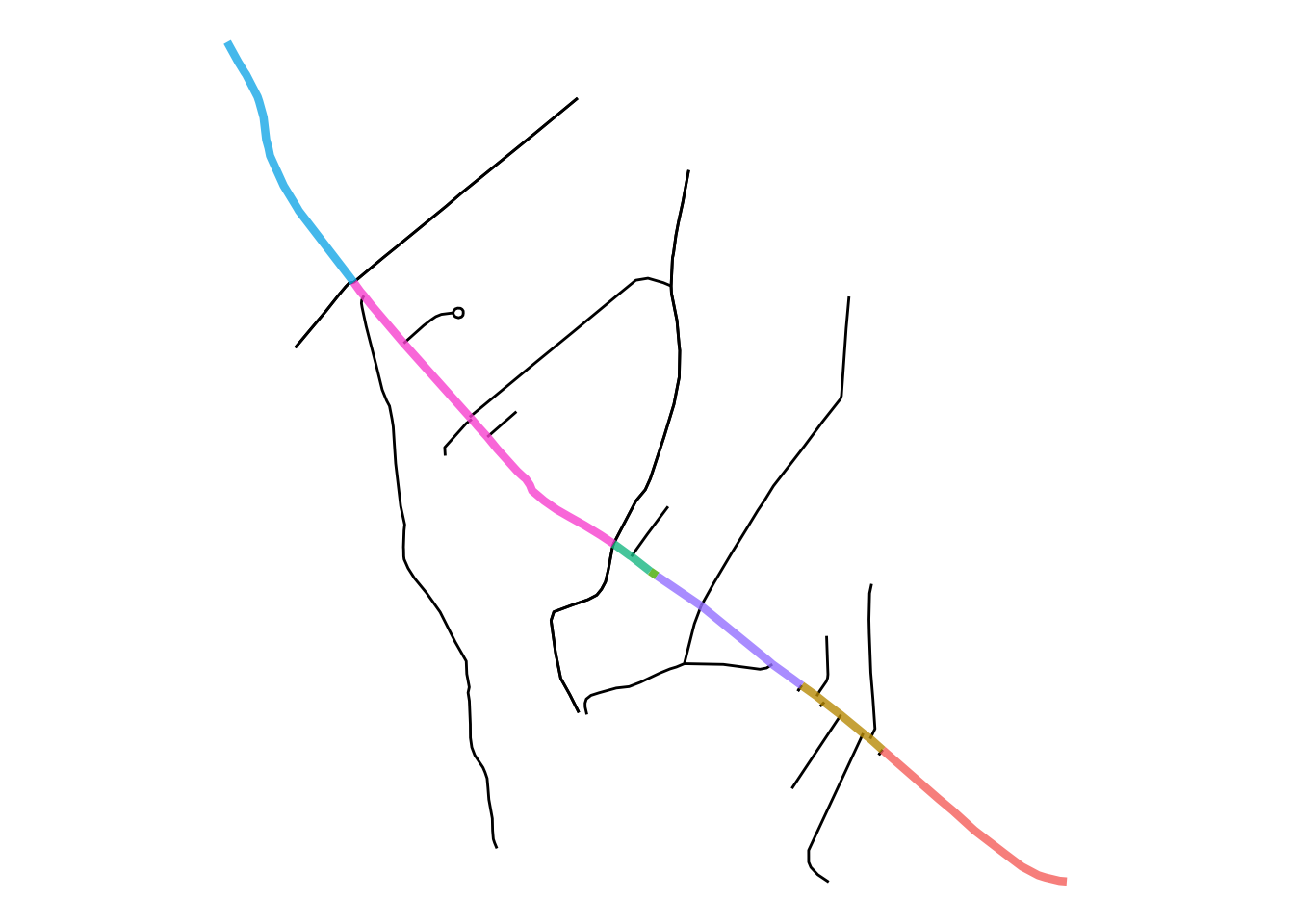
FIGURE 9.10: Bakerloo line, stations, and relevant crimes
Like last time, we can use the st_nearest_feature() function to snap the crimes (in blue) to the line segments. This time, we can do the same, but snap to the points (the stations) instead. This will return, for each point, the ID of the nearest station.
bk_stn_crimes <- st_nearest_feature(bakerloo_crimes, bakerloo_stops)In this object, we see that we now have the stop ID for the closest stop to each crime incident. Now we need to count the frequency of each stop ID (as this tells us the number of crimes that are close to it, therefore assigned to it), and join this to our stops dataframe, just like we did with the lines earlier:
#make list of nearest into df of frequency
stops_w_crimes <- as.data.frame(table(bk_stn_crimes))
#join to sections object
bakerloo_stops <- left_join(bakerloo_stops %>% mutate(stopid = rownames(.)),
stops_w_crimes,
by = c( "stopid" = "bk_stn_crimes")) %>%
mutate(Freq = replace_na(Freq, 0)) %>% # replace NAs with 0s
rename(num_violent_crimes = Freq) # rename Freq variable to num_crimesNow we have a dataframe of each stop and the number of crimes that happened closest possibly to it. We could make a street profile of it with this count (in fact we will in a moment) but first let’s discuss about ratesfor nodes.
9.5.2 Calculating a rate for nodes
In order to calculate a crime rate for each station, we need to think about what is an acceptable denominator. How can we best estimate the number of opportunities present for the particular crime type we are interested in, and how might that be captured in some available data set? For our line segments, we could use length as a denominator, and we had an outcome of the crimes per meter length of the line segment. However, there is no such value for our stations (and for other nodes, such as street junctions). So instead, we need to get creative in finding an appropriate denominator for our nodes. Solymosi et al. (2017) considered the various types of denominators that may be available to crime analysts focusing on estimating ambient populations to calculate crime risk. These can be:
- residential population in the area surrounding the station (available from the Census)
- workplace population in the area surrounding the station (also available from the Census)
- number of lines passing through each station (available from station information, or even a network map)
- number of trains passing through each station (available from station information, maybe a timetable)
- number of passengers entering/exiting each station (available from transit authority, maybe via a survey like the Rolling Origin Destination Survey, or smartcard data (eg Oyster card in London))
- and possibly some other options that we have not thought of.
In the case of London underground, we can make use of the Rolling Origin Destination Survey data, which tells us about the number of people entering, exiting, and travelling through each station. We can download this directly from TfL API portal mentioned above, but here again we have provided it. Specifically we are after the file: Total entries and exits by borough-time of day 2017.xls, which contains entry and exit data for each station. As it is an Excel file, we will use the function read_xls() from the readxl library to import it.
The entry and exit data sets are two separate sheets in this excel file, so we will have to read them in one sheet at a time, using read_xls() function from the readxl package. From having seen the data before, we also know that 1) the variable names are in line 4 so we can skip up to there (the skip= argument in the read_xls() function), 2) that the names are messy, so we clean them up using the clean_names() function in the janitor package, and 3) that for some reason the ‘station’ variable is in two columns, so we have to name these as station number and station name using rename() function in the dplyr library (loaded earlier).
#load entries and exits data
#first entries
rods_entries <- read_xls("data/Total entries and exits by borough-time of day 2017.xls",
sheet = "entries", skip = 4, col_names = TRUE) %>%
clean_names() %>% rename(stn_num = station, stn_name = x3)
#then exits
rods_exits <- read_xls("data/Total entries and exits by borough-time of day 2017.xls",
sheet = "exits", skip = 4, col_names = TRUE) %>%
clean_names() %>% rename(stn_num = station, stn_name = x3)Then finally we can link the entry and exit data together with left_join() from dplyr, and sum them together to get the whole day’s worth of entries and exits (because we don’t care about time of day for our purposes here) using group_by() and summarise(), then create a final variable called total_pax using the mutate() function. The total_pax variable tells us how many trips we can expect to go through that station on a given day, giving us a nice denominator to calculate crime rate.
rods <- rods_exits %>%
left_join(., rods_entries) %>% # join up the exit and entry data
group_by(borough, stn_num, stn_name) %>% # sum all time periods within the day
summarise(total_exiting = sum(number_exiting),
total_entering = sum(number_entering)) %>%
filter(stn_num != "Total for borough") %>% # remove the borough totals
mutate(total_pax = total_exiting + total_entering) # create grand total of pax tripsNow we have our denominator for calculating the crime rate. Let’s join it to our Bakerloo Line stations to do so.
bakerloo_stops <- left_join(bakerloo_stops, rods)Now we can calculate the rate by dividing the number of crimes (num_crimes) by the total number of daily passengers (total_pax), and let’s times by 10,000 to get crimes per 10,000 passengers for each station.
bakerloo_stops$violent_crime_rate <- bakerloo_stops$num_violent_crimes/
bakerloo_stops$total_pax * 10000Our top station for violent and sexual offences is Edgware Road, which has 34.4 such crimes per 10,000 passengers, while our lowest are the stations which recorded 2 crimes per 10,000 passengers (Warwick Avenue). Great, now let’s actually visualise crime along the stations of the Bakerloo Line using Street Profile Analysis!
9.5.3 Visualising with Street Profile Analysis
We have (almost) everything we need to visualise crime along the Bakerloo line using Street Profile Analysis. What we want to do, is imagine the Bakerloo line is the x axis, and then use the y axis to show the crime rate. Of course for this, we want to know the order in which the stations follow each other. Annoyingly, at the time of writing, the TfL API doesn’t actually have any sort of sequence information with the stops so we have to make our own lookup table:
bakerloo_order <- data.frame( stop_num = c(1:25),
stn_name = c("Harrow & Wealdstone",
'Kenton',
'South Kenton',
'North Wembley',
'Wembley Central',
'Stonebridge Park',
'Harlesden',
'Willesden Junction',
'Kensal Green',
"Queen's Park",
'Kilburn Park',
'Maida Vale',
'Warwick Avenue',
'Paddington',
'Edgware Road',
'Marylebone',
'Baker Street',
"Regent's Park",
'Oxford Circus',
'Piccadilly Circus',
'Charing Cross',
'Embankment',
'Waterloo',
'Lambeth North',
'Elephant & Castle')
)In other cases you might have some sort of sequence information, or you might need to make a different sequence. For example, if you are plotting your Street Profile Analysis of a major roadway, like Spicer et al. (2016), you might want to list the streets which intersect it, in order from one end to the other. Once the ordered list exists, we can join this to the original dataframe to have a sequence to order our stops by:
bakerloo_stops <- left_join(bakerloo_stops, bakerloo_order)And then we can use this to order our stop names, and finally present the Street (or rather Route) Profile for the Bakerloo line considering violent and sexual offences:
ggplot(bakerloo_stops,
aes(x = reorder(stn_name, stop_num),
y = violent_crime_rate,
group = line)) +
geom_point() +
geom_line() +
xlab("Bakerloo Line") +
ylab("Crime Rate per 10,000 passengers") +
theme_bw() +
theme(axis.text.x = element_text(angle = 60, hjust = 1))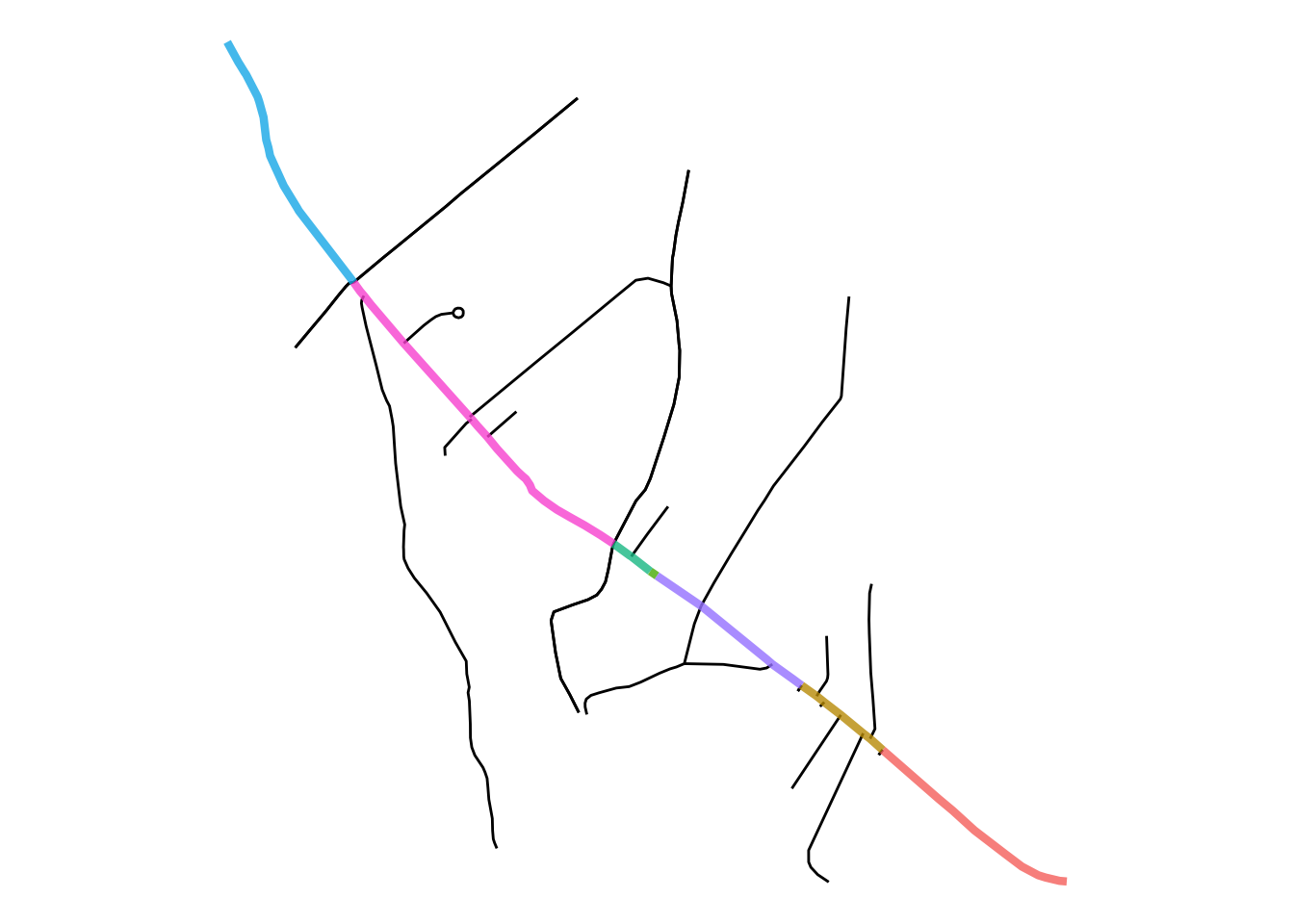
FIGURE 9.11: Route profile for Bakerloo line
This is a non-geographical way to visualise crime rates along micro places, while still taking into account some spatial information, namely the sequence of these nodes along our line segment. Surely we could prettify the plot with additional code, but with this cruder version you can see what the street profile gives you.
What is really a strength of Street Profile Analysis is that you can compare different things along the same route, which may be difficult to compare on a two-dimensional map. For example, we could compare how crime changes along the network between different months of the year here. For this, we can create a dataframe of crimes per month for each station. For each crime find the nearest station (st_nearest_feature()) and assign the station id to a new column, then group by month and nearest station.
monthy_crimes <- bakerloo_crimes %>%
mutate(nearest_stn_id = st_nearest_feature(bakerloo_crimes, bakerloo_stops)) %>%
st_drop_geometry() %>%
group_by(nearest_stn_id, month) %>%
count() %>%
pivot_wider(names_from = month, values_from = n) %>%
left_join(bakerloo_stops, ., by = c("stop_num" = "nearest_stn_id")) %>%
replace(is.na(.), 0)And now we can compare between different months by adding each month on as a ggplot layer. For example, if we wanted to see January, February, and March:
ggplot(monthy_crimes, aes(x = reorder(stn_name, stop_num), group = line)) +
geom_point(aes(y = `2019-01`, col = "Jan")) +
geom_line(aes(y = `2019-01`, col = "Jan")) +
geom_point(aes(y = `2019-02`, col = "Feb")) +
geom_line(aes(y = `2019-02`, col = "Feb")) +
geom_point(aes(y = `2019-03`, col = "Mar")) +
geom_line(aes(y = `2019-03`, col = "Mar")) +
xlab("Bakerloo Line") +
ylab("Crime Rate per 10,000 passengers") +
theme_bw() +
theme(axis.text.x = element_text(angle = 60, hjust = 1)) +
scale_colour_manual(values=c("#66c2a5", "#8da0cb", "#fc8d62"),
labels = c("Jan", "Feb", "Mar"),
guide="legend", name="Month")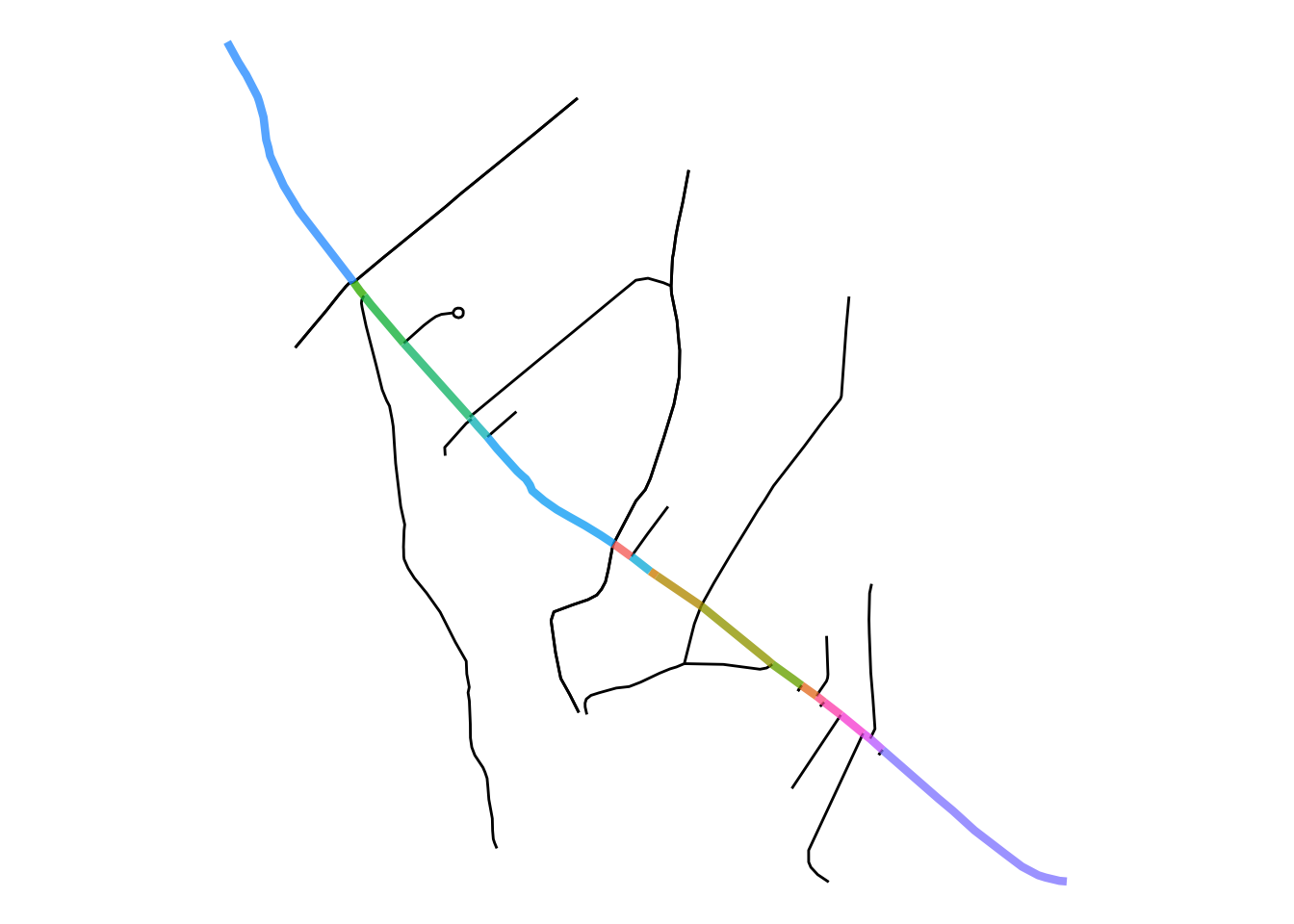
FIGURE 9.12: Route profile of Bakerloo line comparing different months
We could also visualise different crime types, or different sources of data, the possibilities are many, and this is where the strength of this method is evident, over a map, where only one variable at one time can be displayed.
9.6 Density estimation along networks
Earlier we showed how you can produce the hot route maps, which conceptually are similar to the thematic maps we used in previous chapters. Another way of estimating the intensity of crime along spatial networks is to use kernel density estimation methods. You could, as we did in Chapter 7, use standard kernel density estimation methods, but this ignores the underlying structure in the data. As Jeremy Gelb indicates in the vignette for spNetwork, there are a number of problems with this cruder approach:
“Calculating density values for locations outside the network is meaningless and the Euclidean distance underestimates the real distance between two objects on the network. Moreover, networks are not isotropic spaces. In other words, it is not possible to move in every direction, but only along the edges of the network” (Gelb 2021).
Smoothing through kernel density estimation in linear networks is an area of active development and a number of approaches have been proposed over recent years, some of which provide a pragmatic (heuristic) solution, but “their properties are not well understood, statistical insight is lacking,” and “computational cost is high” (McSwiggan, Baddeley, and Nair 2016: 325). The existing software implementation of the “traditional” algorithms that have been developed can deal with small datasets, but may become prohibitive when dealing with larger datasets. More recent algorithms aim to provide faster solutions for larger datasets without seriously compromising performance (see Rakshit et al. (2019)). You can currently do this in R with at least two separate packages spatstat and the newer spNetwork. For reasons of space, given that it provides a more general framework for point pattern analysis and a wider selection of (more principled) approaches, we will only cover spatstat here.
In spatstat a point pattern on a linear network is represented by an object of class lpp (stands for point pattern in a linear network). The functions lpp() and as.lpp() convert raw data into an object of class lpp. The two needed arguments are a matrix or data frame with the coordinates of the points (or alternatively a ppp object that we discussed in chapter 7) and a liner network of class linnet).
The linnet object will represent the network of a set of line segments, containing information about each of these segments (edges) and its vertices (nodes). You can generate a linnet object from a SpatialLines (sp) object using functions from maptool, specifically as.linnet.SpatialLines(). If you need to process this network before is ready you can do so with some functions from spatstat or SpnetPrep as preferable (and only then create your linnet object).
We will show here how to transform a SpatialLines object into linnet and how, then, we generate a lpp object. First, we will get the road network for a few census tracts in Englewood, one of the community areas in Chicago with a high crime rate (see Briz-Redón, Martı́nez-Ruiz, and Montes (2019a) for a similar example that inspired ours). To do this we will use the tigris package, that provides both the road network data and the census geographies as shown in the code below. We then use the intersect() function from the raster package to only get the fractions of the roads covered by the census tracts we have selected. Then we need to get this into a projected coordinate system so that we can use spatstat. The final step is to turn this sp object into a linnet object using as.linnet.SpatialLines() from the maptools package.
# get the road network and census tracts for Cook county in Illinois
# the tracts we get as sf for easier filter and then turn into sp
cook_roads <- roads(state = "Illinois", county = "031", class="sp")
# select census tracts based on their id code
cook_tract <- tracts(state = "Illinois", county = "031") %>%
filter(TRACTCE == "681100" | TRACTCE == "681400" |
TRACTCE == "681200" | TRACTCE == "681300" )
# transform to sp object
cook_tract <- as(cook_tract, "Spatial")
# filter the roads to only the census tract coverage
tract_roads <- raster::intersect(cook_roads, cook_tract)
# reproject the sp object
x <- CRS(SRS_string='EPSG:6454')
tract_roads <- spTransform(tract_roads, x)
s_englewood_linnet <- as.linnet.SpatialLines(tract_roads)
# tidy up no longer needed objects and plot
rm(list = c("cook_roads", "cook_tract", "tract_roads","x" ))Now we have our linnet object called s_englewood_linnet which contains a street network for the South Englewood area. We can plot this to have a visual inspection.
plot(s_englewood_linnet, style = "none", main = "South Englewood")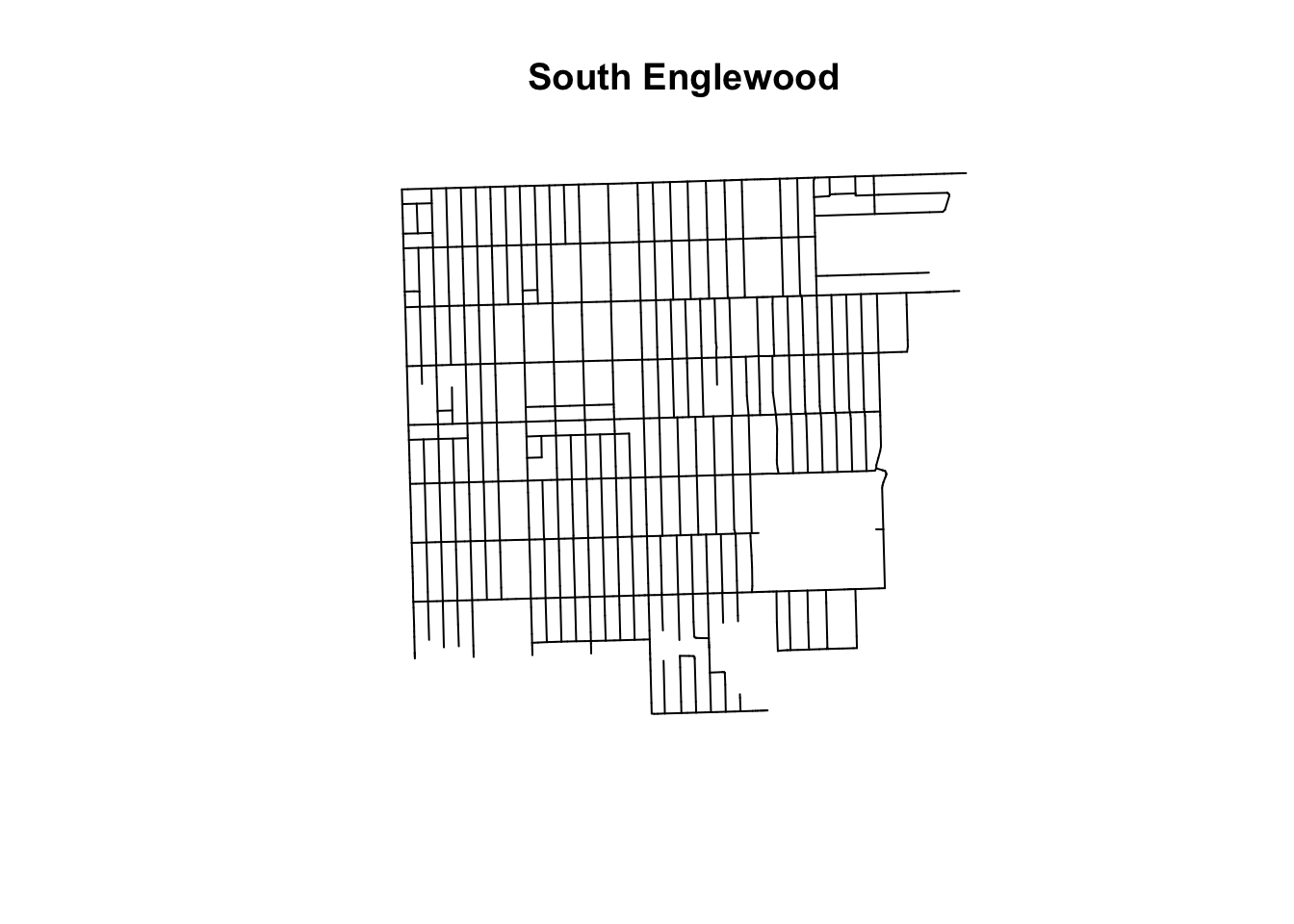
FIGURE 9.13: Street network of South Englewood as linnet object
Now we need to put some crime data in this street network. For that we will rely on the crimedata package we introduced in the previous chapter. We will take this data and first will create a ppp object using as a window the bounding box of the ´linnet` object we just created and that you can see by printing it:
s_englewood_linnet## Linear network with 1149 vertices and 1351 lines
## Enclosing window: rectangle = [356456, 358379] x
## [565240, 567094] unitsThe code for getting the data has been covered before so we don´t annotate it nor provide a detailed explanation here. We are extracting the assaults for the summer of 2019 and the Englewood community area. Just to note we are using as.ppp() since the standard ppp function retains in the created object the points outside the bounding box (even if this only affects the plotting, which will plot all).
# get chicago crime data
chicago_viol <- get_crime_data(cities = "Chicago", years = 2019, quiet = TRUE,
type = "extended", output = "sf") %>%
# select only assaults
filter((offense_type == "aggravated assault" | offense_type == "simple assault") &
# select only area of interest
chi_community_area == "68")
# transform to projected CRS
chicago_viol <- st_transform(chicago_viol, 6454)
# create a variable for month and keep only June to August
chicago_viol <- chicago_viol %>%
mutate(month = month(date_single)) %>%
dplyr::filter(month %in% (6:8))
# create matrix of coordinates for our violent crimes
chi_viol_coord <- matrix(unlist(chicago_viol$geometry), ncol = 2, byrow = T)
# create window
w <- as.owin(c(356456.4, 358379.1,565240.1, 567094.3))
# create ppp object
chi_viol_ppp <- ppp(x = chi_viol_coord[,1], y = chi_viol_coord[,2],
window = w, check = T)
chi_viol_ppp <- as.ppp(chi_viol_ppp)
#we know there is multiplicity so we will add this as a mark
marks(chi_viol_ppp) <- multiplicity(chi_viol_ppp)Now that we have the ppp object we can use it to create our lpp object (notice that, as noted above, there are other ways to input your points when creating a lpp object) and then plot it. There are a 264 locations, some of which represent up to 6 incidents. Remember that this is likely the result of geomasking due to privacy concerns.
chi_viol_lpp <- lpp(chi_viol_ppp, s_englewood_linnet)Now we can plot our two layers, the crimes in our chi_viol_lpp object, and the network in the s_englewood_linnet object.
plot(chi_viol_lpp, meansize = 50, main = "Assaults in South Englewood (2019)")
plot(s_englewood_linnet, style = "none", add= TRUE)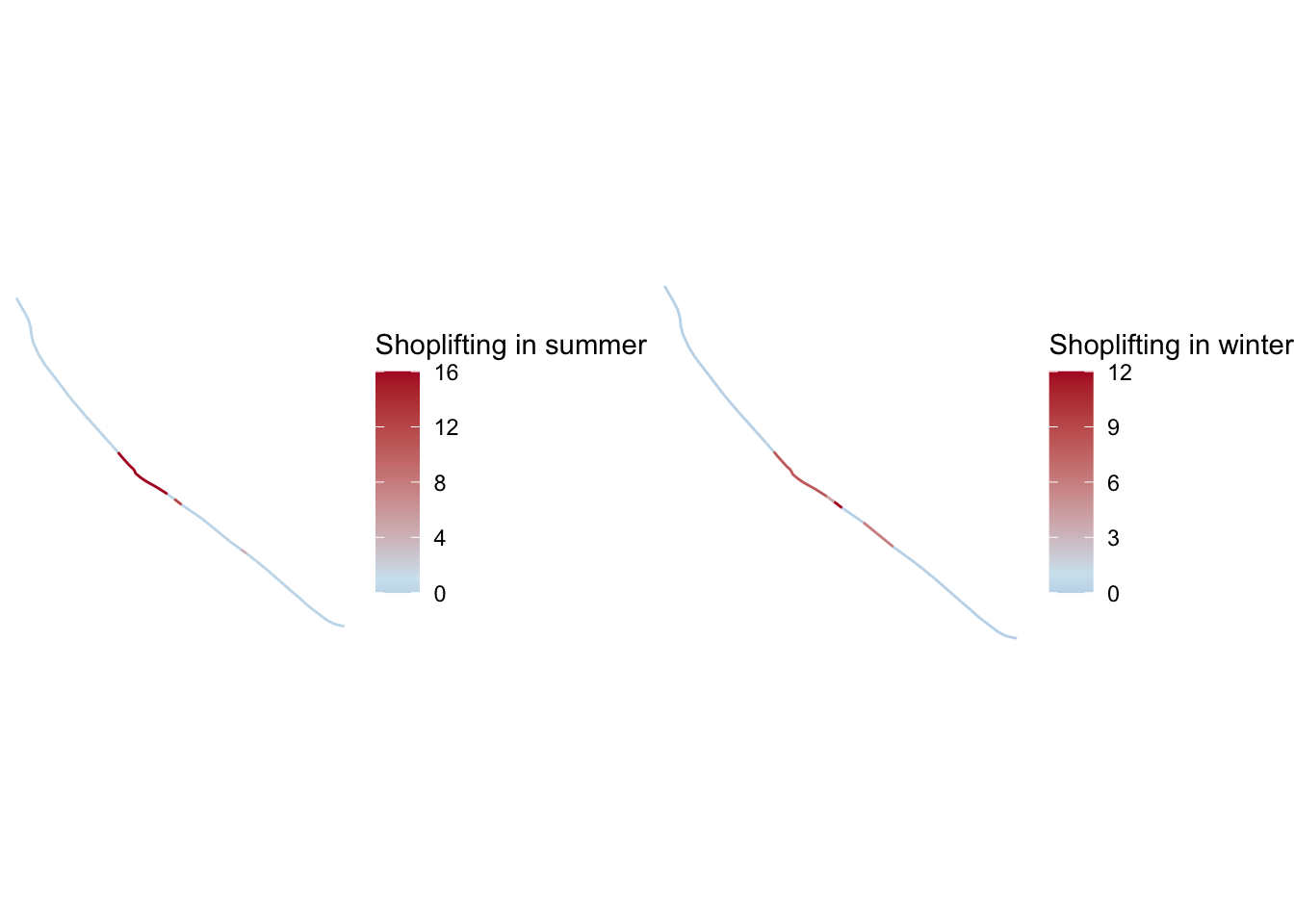
FIGURE 9.14: Assaults as lpp object over network as linnet object
A lpp object contains the linear network information, the spatial coordinates of the data points, and any number of columns of marks (in this case the mark is telling us the type of crime we are dealing with). It also contains the local coordinates seg and tp for the data points. The local coordinate seg is an integer identifying the particular street segment the data point is located in. A segment is each of the sections of a street between two vertices (marking the intersection with another segment). The local coordinate tp is a real number between 0 and 1 indicating the position of the point within the segment: tp=0 corresponds to the first endpoint and tp=1 correspond to the second endpoint.
The visual inspection of the map suggest that the intensity of crime along the network is not spatially uniform. Like we did before, we can estimate the density of data points along the networks using Kernel estimation with density.lpp(). This is an area of spatstat that has seen significant development in the latest release. Depending on the arguments passed to the function a different algorithm will be employed to estimate the density. Alternatively one could use the new specific functions for each of these different algorithms: densityQuick() (see Rakshit et al. (2019)), densityEqualSplit() (see Okabe and Sugihara (2012)), or densityHeat() (see McSwiggan, Baddeley, and Nair (2016)).
The Okabe-Suhigara method was the first to be developed for this kind of applications and can be invoked with densityEqualSplit(). We can specify the kernel (the default is epanechnikov) and the smoothing bandwidth, sigma (the standard deviation of the kernel). Here, we are going for 60 meters for illustration, but see Chapter 7: Spatial point patterns of crime events in this book for details on these parameters). There are two versions of this algorithm, the continuous that is excruciatingly slow (particularly for larger datasets) and the discontinuous that is a bit quicker but has less desirable statistical properties. We are using the number of events per point as the weight for computation, and wrapping everything on system.time() to provide a notion of computation time. We will only show the discontinuous version.
system.time(d_okabe <- densityEqualSplit(chi_viol_lpp,
weights = marks(chi_viol_lpp),
sigma = 60,
continuous = FALSE,
verbose= FALSE))## user system elapsed
## 7.011 0.049 7.089And to visualise:
plot(d_okabe, main="Okabe-Suhigara (disc.)")
FIGURE 9.15: Network density map (Okabe-Suhigara (disc.) method)
McSwiggan, Baddeley, and Nair (2016) subsequently developed an algorithm that is equivalent to the Okabe-Suhigara method using the continuous rule applied to the Gaussian kernel, and therefore has more desirable properties than the equal split discontinuous, but that runs faster (than the Okabe-Suhigara equal split continuous version).
system.time(d_mcswiggan <- densityHeat.lpp(chi_viol_lpp,
weights = marks(chi_viol_lpp),
sigma = 60))## user system elapsed
## 286.84 58.84 349.39plot(d_mcswiggan, main="McSwiggan")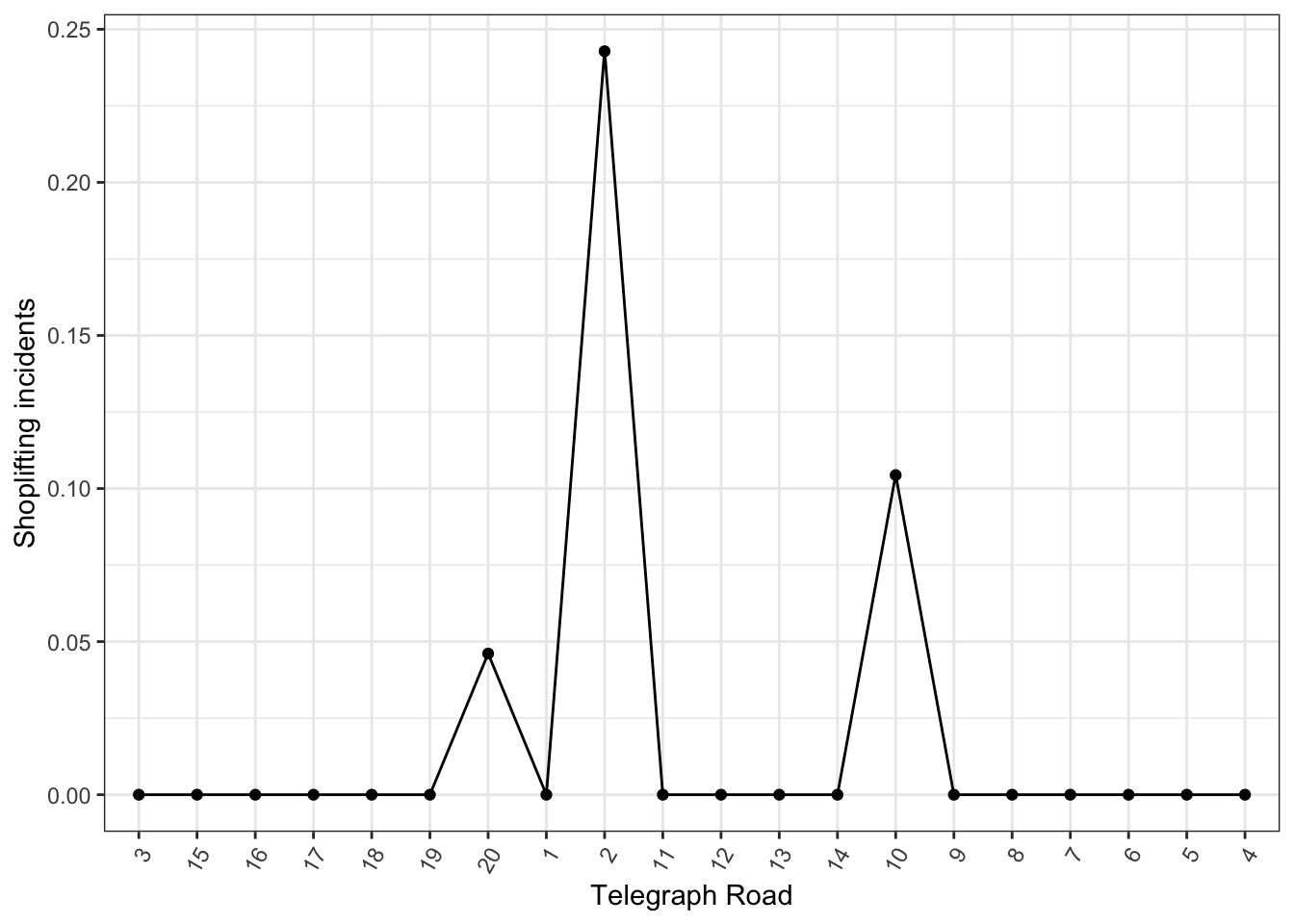
FIGURE 9.16: Network density map (McSwiggan Gaussian method)
Finally, as noted above, Rakshit et al. (2019) developed a fast algorithm, using a convolution method, that is particularly helpful with large datasets. The analysis of the authors suggest this estimator “is consistent, and its statistical efficiency is only slightly suboptimal” (Rakshit et al. 2019).
system.time(d_rakshit <- densityQuick.lpp(chi_viol_lpp,
weights = marks(chi_viol_lpp),
sigma = 60,
edge2D = TRUE))## user system elapsed
## 0.105 0.011 0.118We can now plot the data and compare the results:
plot(d_rakshit, main="Rakshit")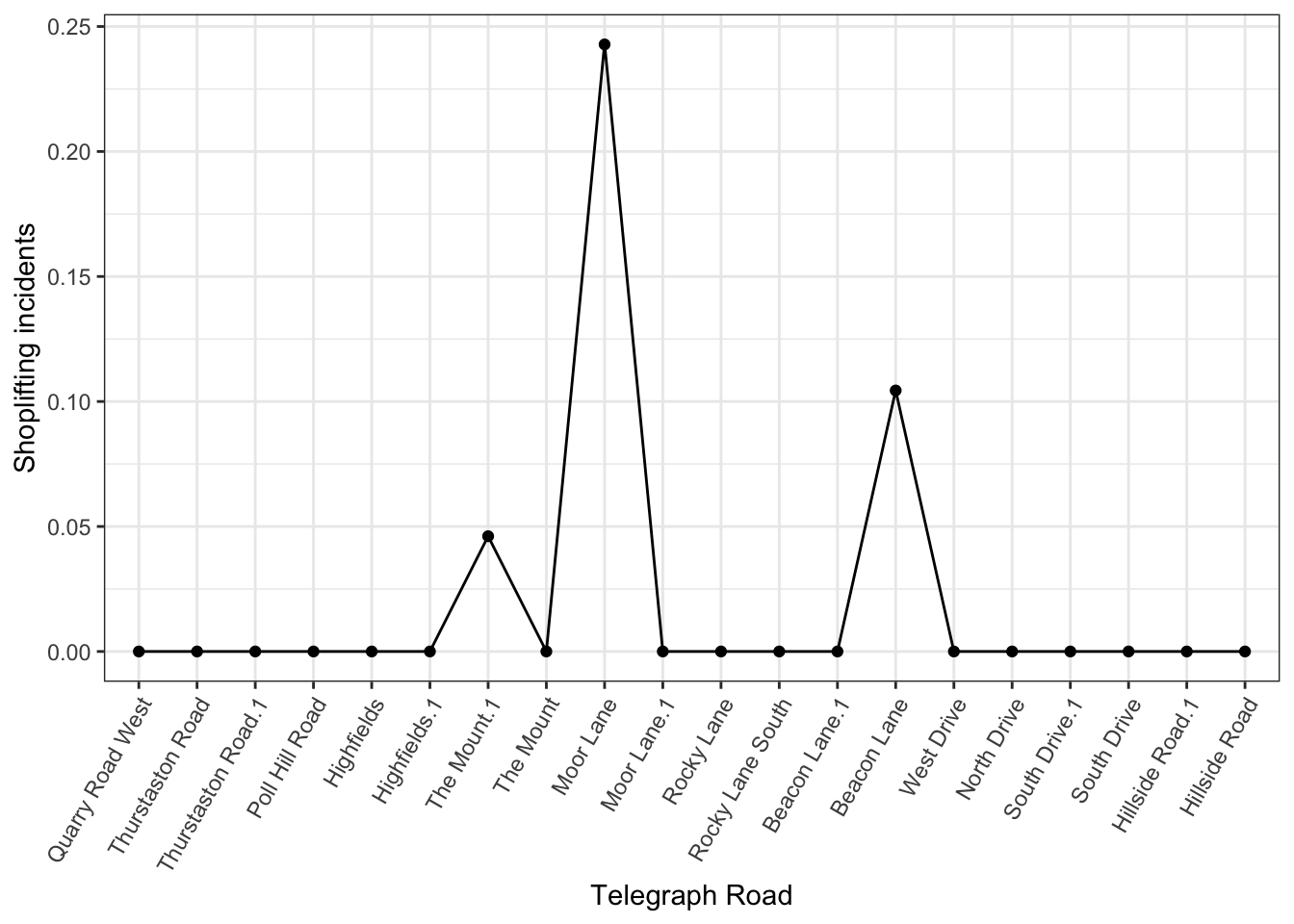
FIGURE 9.17: Network density map (Rakshit method)
So these are some ways in which we can create a density map of crime along networks. You can compare the three maps to see how choice of method affects conclusions. This is something we must always reflect on, when applying these techniques.
9.7 Summary and further reading
The focus in this chapter has been to introduce the issue of crime events along a network. There has been increasing recognition in recent years that the spatial existence of many phenomena is constrained by networks. We have discussed some of the issues associated with the storage, handling, and visualisation of this kind of data. Chapter 1 of Okabe and Sugihara (2012) provides a fairly accessible introduction to the relevance of point pattern data along a network, whereas Chapter 3 offers a slightly more technical discussion of the computational issues associated with the statistical analysis of points along a network. The first few sections of Chapter 17 of Baddeley, Rubak, and Turner (2015) provides background and very useful detail on the way that spatstat handles and stores point pattern data in a network. Baddeley et al. (2021) offers an excellent overview of the challenges of analysing this kind of data and the available methods we have. This overview can also offers an excellent framework to understand the issues of clustering and detection of local clusters along networks to which we will return in the next two chapters.
But spatial networks analysis is a more general area, with various other applications that we could not explore in detail here. O´Sullivan (2014) provides an introduction to spatial network analysis, basically a translation of social network metrics and concepts applied to spatial networks. This kind of perspective is particularly helpful within transport, routing, and similar applications. See, for example, the kind of functionality and applications provided by stplanr. We are also witnessing cross fertilisation between social network analysis and spatial analysis. In epidemiology, for example, we see how this is done for studying the transmission of disease through personal and geographic networks (see, for example, Emch et al. (2010)). Whereas Radil, Flint, and Tita (2010) and Tita and Radil (2011) offer some criminological examples (focused on the study of gangs) linking social network analysis and spatial analysis. Along these lines, the package spnet facilitates the rendering of social network data into a geographical space. Some of these applications can be relevant for investigative crime analysis and other criminological uses. Finally, another way in which social networks are being used within the context of environmental criminology is in contributing to the alternative specifications of neighbourhoods that aim to move beyond the traditional use of census geographies (see Hipp, Faris, and Boessen (2012) and Hipp and Boessen (2013)). Finally, it is also worth exploring the literature on space syntax and crime, and the various analysis that are looking at the structural characteristics of the street network (such as betweenness) and how it influences crime (Toby Davies and Bowers 2018; Kim and Hipp 2019).